Phân Tích Hồi Quy - Nền Tảng Của Dự Đoán Dữ Liệu và Ra Quyết Định

Phân tích hồi quy là gì? Đây không chỉ là một khái niệm khô khan trong thống kê mà còn là “chìa khóa” giúp giải mã những bí ẩn ẩn sau các con số. Khi dữ liệu ngày càng trở thành lợi thế cạnh tranh trong kinh doanh, tài chính, y tế hay khoa học xã hội, việc nắm vững phân tích hồi quy sẽ giúp bạn khám phá mối liên hệ giữa các biến số và đưa ra những quyết định sáng suốt hơn. Vậy điều gì khiến phương pháp này trở nên đặc biệt? Cùng Citinews khám phá ngay nhé!

1. Phân tích hồi quy là gì?

Phân tích hồi quy là phương pháp thống kê giúp xác định và định lượng mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập. Mục tiêu chính của phân tích hồi quy là xây dựng một mô hình toán học phản ánh mức độ và chiều hướng tác động của các biến độc lập lên biến phụ thuộc, từ đó hỗ trợ việc dự đoán, ra quyết định hoặc kiểm định giả thuyết.

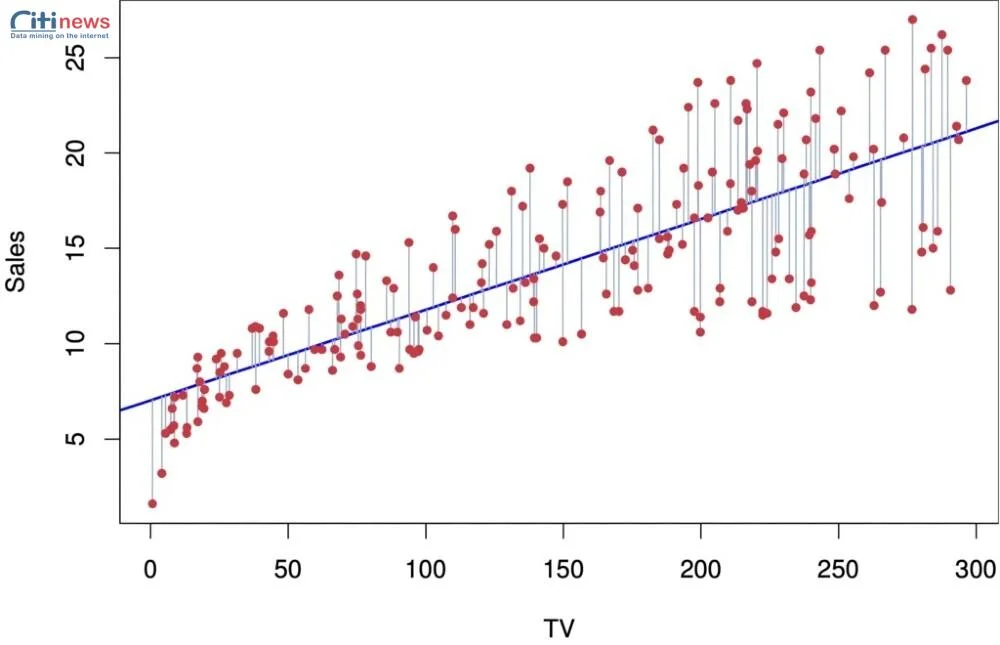
Một trong những dạng đơn giản và phổ biến nhất là hồi quy tuyến tính đơn, trong đó mối quan hệ giữa hai biến được biểu diễn bằng một đường thẳng. Khi phân tích với nhiều biến độc lập, ta gọi là hồi quy tuyến tính bội. Ngoài ra, trong trường hợp dữ liệu phức tạp hơn, khi mối quan hệ giữa các biến không tuân theo tuyến tính, có thể áp dụng hồi quy phi tuyến.

Phân tích hồi quy được ứng dụng rộng rãi trong các lĩnh vực như kinh tế, tài chính, marketing, khoa học xã hội… giúp trả lời các câu hỏi như: yếu tố nào ảnh hưởng nhiều nhất đến kết quả? Tác động đó là tích cực hay tiêu cực? Và mô hình có độ tin cậy đến đâu?

1.1. Những đặc điểm chính của phân tích hồi quy

Dưới đây là những đặc điểm chính của phân tích hồi quy:

• Là kỹ thuật thống kê giúp tìm hiểu mối quan hệ giữa biến phụ thuộc và biến độc lập.
• Cho biết mức độ thay đổi của biến phụ thuộc theo sự biến động của các biến độc lập.
• Xây dựng “đường hồi quy” (best-fit line) – biểu diễn mối liên hệ tối ưu giữa các biến.
• Ứng dụng rộng rãi trong kinh tế, tài chính, marketing…
• Phụ thuộc vào các giả định thống kê như tuyến tính, độc lập, phân phối chuẩn, phương sai không đổi.

1.2. Tại sao lại gọi phương pháp này là "hồi quy"?

Thuật ngữ "hồi quy" (regression) được cho là bắt nguồn từ công trình của Sir Francis Galton vào thế kỷ 19. Khi nghiên cứu dữ liệu sinh học, đặc biệt là chiều cao của con người trong một quần thể, ông nhận thấy rằng chiều cao của con cái thường có xu hướng "hồi quy" về mức trung bình của quần thể, thay vì tiếp tục lệch xa như cha mẹ. 

Nói cách khác, dù có những cá nhân rất cao hoặc rất thấp, phần lớn sẽ phân bố quanh một mức trung bình nhất định. Hiện tượng này được Galton mô tả là "regression to the mean" – hồi quy về giá trị trung bình, và từ đó, tên gọi của phương pháp phân tích thống kê này ra đời.

1.3. Mục đích của phương pháp hồi quy là gì?

Phân tích hồi quy được sử dụng trong thống kê để xác định mối liên hệ giữa các biến trong tập dữ liệu. Không chỉ giúp xác định xem mối liên hệ đó có tồn tại hay không, hồi quy còn cho biết mức độ ảnh hưởng giữa các biến và đánh giá ý nghĩa thống kê của mối quan hệ đó. 

Nhờ khả năng chỉ ra xu hướng và mức độ tác động giữa các biến, phương pháp hồi quy trở thành một công cụ mạnh mẽ trong suy luận thống kê và được ứng dụng rộng rãi trong việc dự đoán kết quả trong tương lai dựa trên dữ liệu quan sát trong quá khứ.

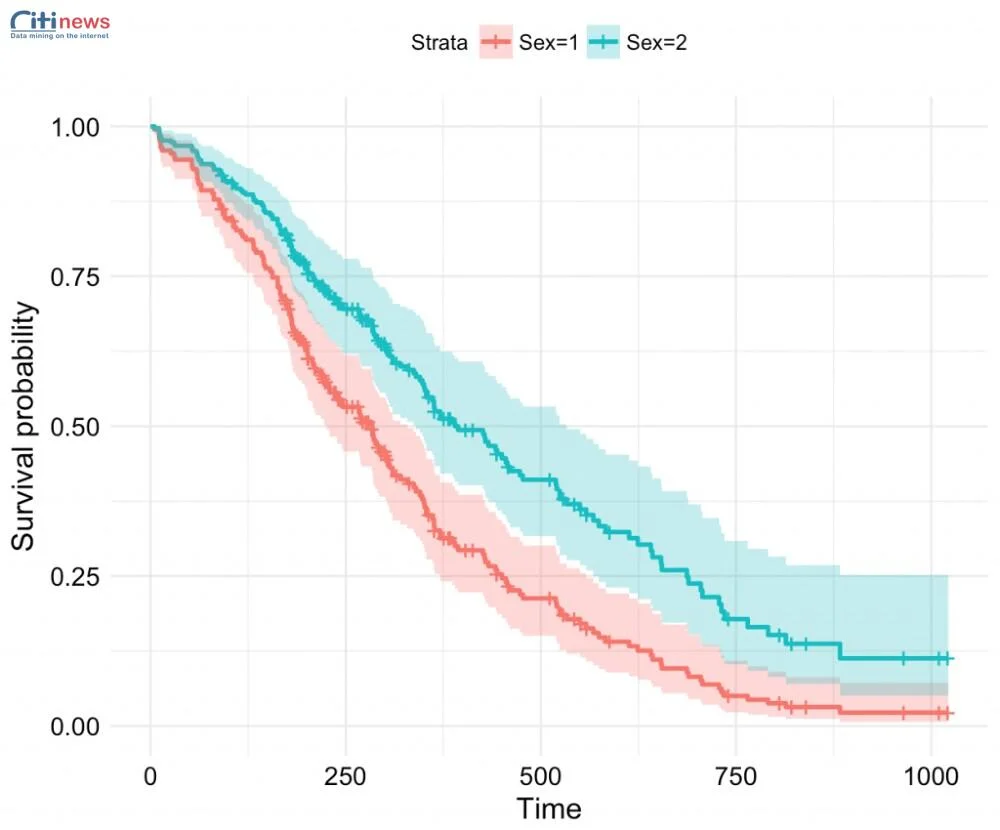
2. Các loại phân tích hồi quy phổ biến

Có nhiều loại phân tích hồi quy, mỗi loại phù hợp với từng loại dữ liệu và mục tiêu nghiên cứu khác nhau. Dưới đây là các loại phân tích hồi quy phổ biến nhất:

1. Hồi quy tuyến tính (Linear Regression)

• Đơn giản (Simple Linear Regression): Một biến phụ thuộc và một biến độc lập.
• Đa biến (Multiple Linear Regression): Một biến phụ thuộc và nhiều biến độc lập.
• Giả định: Mối quan hệ tuyến tính giữa các biến, phân phối chuẩn, phương sai không đổi.

2. Hồi quy logistic (Logistic Regression)

Dùng khi biến phụ thuộc là nhị phân (0 hoặc 1, ví dụ: có bệnh/không bệnh).

Có thể mở rộng thành:

• Hồi quy logistic đa thức (Multinomial Logistic Regression): Cho biến phụ thuộc có nhiều hơn 2 nhóm phân loại.
• Hồi quy logistic thứ tự (Ordinal Logistic Regression): Cho biến phụ thuộc dạng phân loại có thứ tự (ví dụ: thấp - trung bình - cao).

3. Hồi quy Poisson

• Dùng cho dữ liệu đếm (ví dụ: số lần xảy ra sự kiện).
• Biến phụ thuộc là số nguyên không âm.
• Giả định phân phối Poisson.

4. Hồi quy Ridge, Lasso và Elastic Net

• Ridge Regression (L2 regularization): Giảm hiện tượng đa cộng tuyến bằng cách thêm phạt vào tổng bình phương hệ số.
• Lasso Regression (L1 regularization): Tương tự Ridge nhưng có thể đưa hệ số về 0, giúp chọn biến tự động.
• Elastic Net: Kết hợp giữa Ridge và Lasso.

5. Hồi quy phi tuyến (Nonlinear Regression)

• Dùng khi mối quan hệ giữa biến phụ thuộc và biến độc lập không tuyến tính.
• Ví dụ: mô hình mũ, logarit, đa thức…

6. Hồi quy phân cấp (Hierarchical Regression)

Dùng để đánh giá mức độ cải thiện của mô hình khi thêm từng nhóm biến độc lập vào theo từng bước.

7. Hồi quy bội (Multivariate Regression)

Mô hình hóa nhiều biến phụ thuộc cùng lúc.

8. Hồi quy robust (Robust Regression)

Dùng khi dữ liệu có nhiễu hoặc ngoại lệ (outlier), giúp giảm ảnh hưởng của điểm lệch.

9. Hồi quy với dữ liệu chuỗi thời gian (Time Series Regression)

Bao gồm các mô hình như: ARIMA, AR, MA, dùng cho dữ liệu biến đổi theo thời gian.

10. Hồi quy tổng quát (Generalized Linear Models - GLM)

Mở rộng hồi quy tuyến tính để xử lý các phân phối khác nhau (nhị phân, đếm, nhị thức âm...).

Bao gồm: Logistic, Poisson, Gamma regression,…

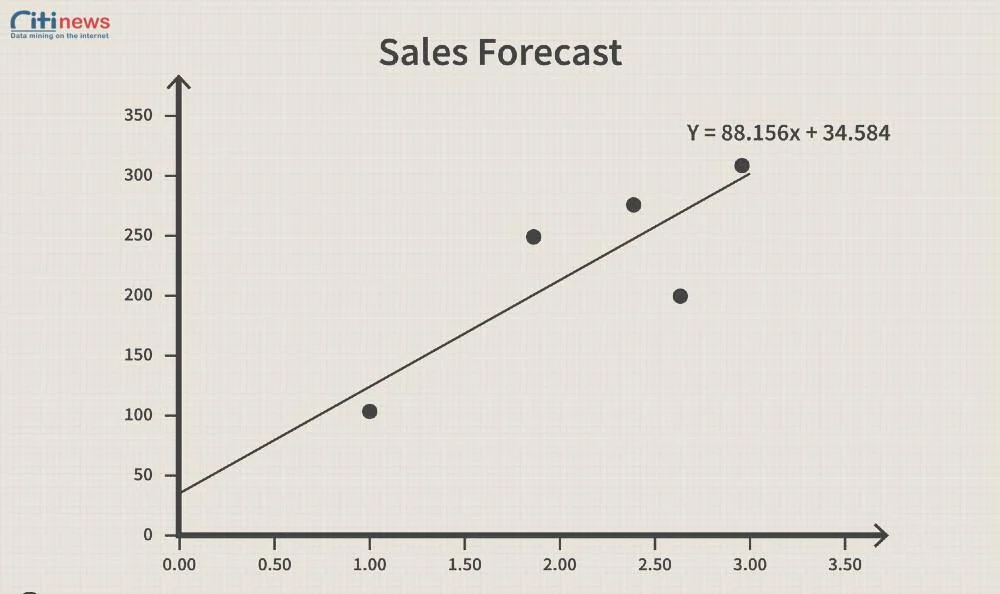
3. Cách phân tích hồi quy hoạt động

Phân tích hồi quy hoạt động bằng cách xác định mối tương quan giữa các biến trong một tập dữ liệu và lượng hóa xem mối tương quan đó có ý nghĩa thống kê hay không. Cụ thể, phương pháp này giúp xây dựng một mô hình toán học — gọi là phương trình hồi quy — mô tả mối quan hệ giữa biến phụ thuộc (biến mà bạn muốn dự đoán) và biến độc lập (các yếu tố được cho là ảnh hưởng đến biến phụ thuộc).

Ví dụ đơn giản nhất là hồi quy tuyến tính đơn, trong đó chỉ có một biến độc lập. Khi bạn thêm nhiều biến độc lập vào mô hình, đó là hồi quy tuyến tính bội. Với các trường hợp dữ liệu phức tạp hơn, có thể áp dụng các mô hình hồi quy phi tuyến để phù hợp với bản chất không tuyến tính giữa các biến.

4. Các bước phân tích hồi quy cơ bản

Để áp dụng phương pháp phân tích hồi quy một cách hiệu quả, bạn cần tuân thủ một quy trình cụ thể. Dưới đây là 5 bước để bạn thực hiện quy trình phân tích hồi quy:

Bước 1: Thu thập dữ liệu

Thu thập số liệu của biến phụ thuộc và các biến độc lập qua nhiều quan sát (chẳng hạn số liệu hàng tháng trong 3 năm gần đây).

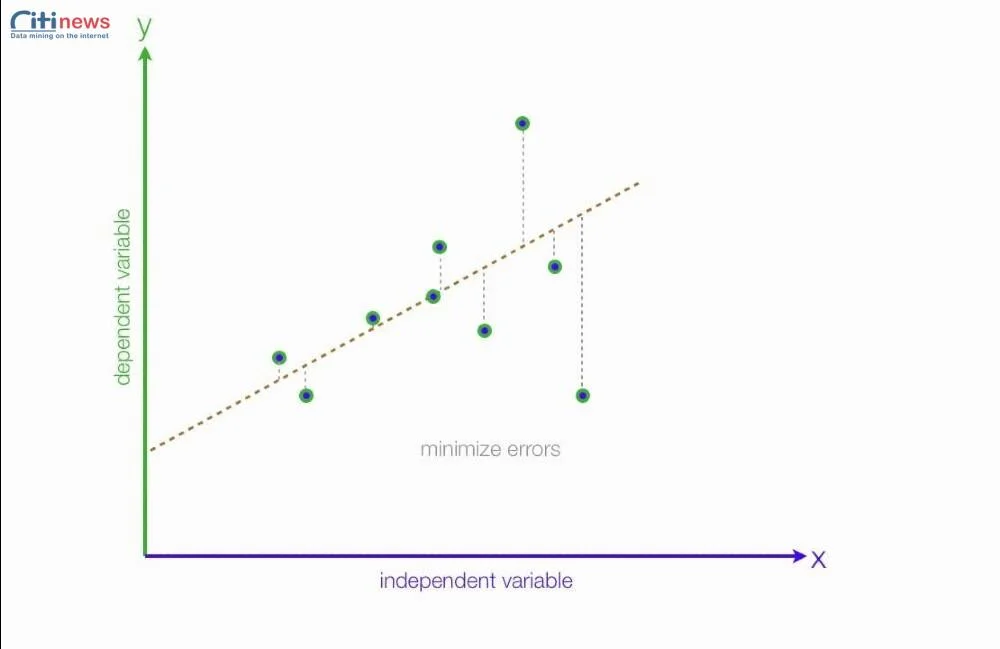
Bước 2: Vẽ biểu đồ phân tán (scatter plot)

Mỗi điểm trên biểu đồ thể hiện mối quan hệ giữa biến độc lập và biến phụ thuộc. Từ biểu đồ, bạn có thể quan sát xem liệu có xu hướng tăng hoặc giảm nào giữa hai biến.

Bước 3: Xây dựng mô hình hồi quy

Sử dụng phần mềm thống kê như Excel, SPSS, R hoặc STATA để tìm ra đường hồi quy — đường thẳng tốt nhất đại diện cho mối quan hệ giữa các biến. Phương trình thường có dạng:

y = a + bx + ε

Trong đó:

• y là biến phụ thuộc (ví dụ: doanh số),
• x là biến độc lập (ví dụ: lượng mưa),
• a là hệ số chặn (giá trị y khi x = 0),
• b là hệ số góc (mức độ thay đổi của y khi x tăng 1 đơn vị),
• ε là sai số (phần mà mô hình không giải thích được).

Bước 4: Phân tích hệ số và sai số

Hệ số b cho biết mức độ ảnh hưởng của biến độc lập lên biến phụ thuộc. Trong khi đó, thuật ngữ sai số (error term) phản ánh độ chính xác của mô hình — nếu sai số lớn, mô hình ít đáng tin cậy hơn.

Bước 5: Mở rộng mô hình

Thay vì chỉ sử dụng một biến độc lập, bạn có thể thêm các yếu tố khác (như khuyến mãi từ đối thủ, xu hướng thị trường...) để tăng độ chính xác. Tuy nhiên, cần cẩn trọng khi thêm quá nhiều biến để tránh nhiễu và mô hình quá phức tạp.

5. Ví dụ về phân tích hồi quy trong tài chính

Ví dụ phân tích hồi quy trong tài chính thường được sử dụng để đánh giá mối quan hệ giữa giá trị của một tài sản với các yếu tố ảnh hưởng như giá hàng hóa, lãi suất, hoặc hiệu suất của các ngành cụ thể. 

Một ví dụ điển hình là mô hình định giá tài sản vốn (CAPM – Capital Asset Pricing Model), vốn dựa trên phân tích hồi quy để ước tính lợi suất kỳ vọng của cổ phiếu và từ đó xác định chi phí sử dụng vốn.

Trong mô hình CAPM, lợi suất của một cổ phiếu sẽ được đem so sánh (hồi quy) với lợi suất của một chỉ số thị trường rộng hơn như S&P 500. Kết quả của quá trình này cho ra hệ số beta – đại diện cho mức độ rủi ro của cổ phiếu so với thị trường chung. Hệ số beta chính là hệ số góc (slope) của đường hồi quy trong mô hình CAPM. Trong đó, lợi suất của cổ phiếu đóng vai trò là biến phụ thuộc (Y), còn phần bù rủi ro thị trường (market risk premium) chính là biến độc lập (X).

Để cải thiện khả năng dự báo của mô hình, người ta có thể bổ sung thêm nhiều biến khác vào CAPM, chẳng hạn như vốn hóa thị trường của cổ phiếu, các tỷ số định giá hoặc lợi suất gần đây. Những biến bổ sung này được gọi là các yếu tố Fama-French – tên gọi bắt nguồn từ hai giáo sư đã phát triển mô hình hồi quy tuyến tính đa biến nhằm giải thích tốt hơn lợi suất của các tài sản. 

Những mô hình mở rộng như Fama-French giúp phân tích hồi quy trong tài chính trở nên linh hoạt và phản ánh tốt hơn các yếu tố thực tế ảnh hưởng đến thị trường.

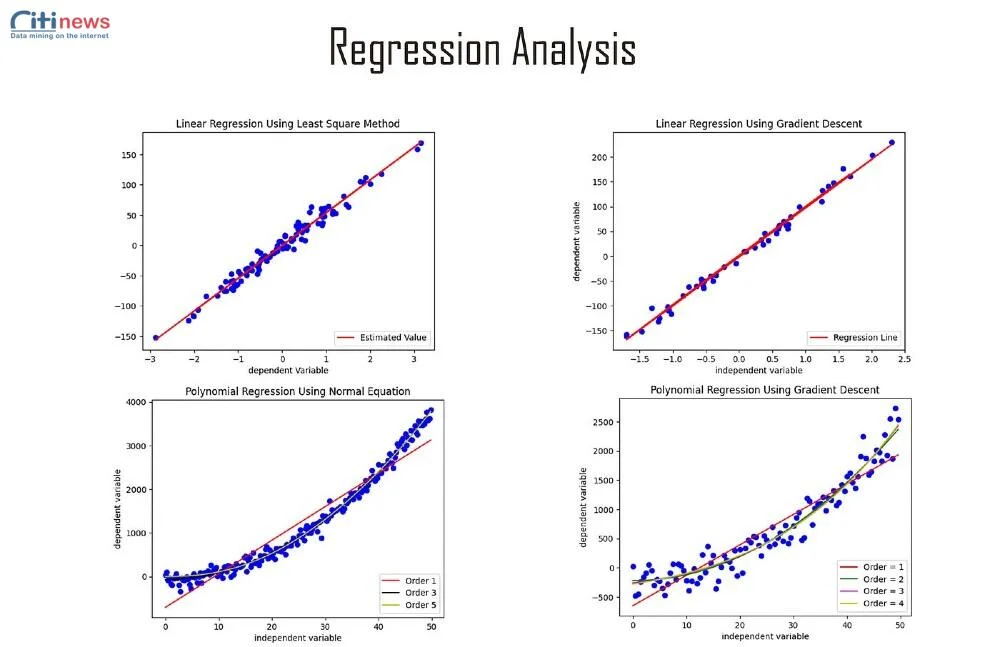
6. Ứng Dụng Phân Tích Hồi Quy Trong Giao Dịch Forex

Trong thị trường Forex, phân tích hồi quy là một phương pháp sử dụng dữ liệu lịch sử để dự đoán giá trị của các yếu tố trong tương lai, từ đó giúp các nhà giao dịch xác định mối quan hệ giữa các biến số. Khi giao dịch ngoại hối, phân tích hồi quy thường được áp dụng để hiểu rõ sự ảnh hưởng của các yếu tố như tỷ giá hối đoái, chỉ số kinh tế, hoặc các yếu tố kỹ thuật đối với giá của cặp tiền tệ.

Phương pháp phân tích hồi quy phổ biến nhất là hồi quy tuyến tính, trong đó một biến phụ thuộc (như giá cặp tiền tệ) được dự đoán dựa trên một hoặc nhiều biến độc lập (chẳng hạn như chỉ số kinh tế hoặc chỉ báo kỹ thuật). Khi sử dụng phân tích hồi quy, nhà giao dịch có thể nhận diện các xu hướng và mức độ mạnh yếu của sự thay đổi giá, qua đó đưa ra quyết định chiến lược giao dịch hợp lý.

Mặc dù phân tích hồi quy không thể đảm bảo dự đoán chính xác tuyệt đối, nhưng nó giúp nhà giao dịch có cái nhìn rõ ràng hơn về xu hướng và các yếu tố tác động đến biến động giá, từ đó tối ưu hóa chiến lược giao dịch của mình.

7. Ưu và nhược điểm của chiến lược hồi quy trong giao dịch forex

Trong giao dịch forex, chiến lược hồi quy là một trong những phương pháp phân tích kỹ thuật phổ biến, đặc biệt được các nhà giao dịch yêu thích khi muốn dự đoán xu hướng dựa trên dữ liệu lịch sử. Tuy nhiên, giống như bất kỳ chiến lược nào khác, hồi quy cũng có những điểm mạnh và hạn chế nhất định. Cùng mình điểm qua các ưu và nhược điểm để xem liệu chiến lược này có phù hợp với phong cách giao dịch của bạn không nhé!

8. Những lỗi thường gặp khi sử dụng phân tích hồi quy

Phân tích hồi quy là công cụ mạnh mẽ trong thống kê và nghiên cứu dữ liệu. Tuy nhiên, nếu sử dụng sai cách, nó có thể dẫn đến những kết luận sai lệch nghiêm trọng. Dưới đây là những lỗi phổ biến – hãy cùng điểm qua để tránh mắc phải nhé!

8.1. Không xác định mục tiêu rõ ràng

Nhiều người quản lý chỉ đạo mơ hồ kiểu “tìm xem điều gì ảnh hưởng đến doanh số” mà không nêu rõ các yếu tố nghi ngờ cụ thể. Khi đó, nhà phân tích dễ “đi câu cá” – tức là dò tìm ngẫu nhiên các mối quan hệ, dẫn đến kết quả sai lệch do ngẫu nhiên.

Ví dụ: tung đồng xu nhiều lần sẽ có lúc ra chuỗi toàn sấp hoặc toàn ngửa – không có nghĩa là có quy luật thật sự.

=>> Bài học: Luôn xác định rõ biến nghi ngờ có ảnh hưởng và tập trung kiểm tra chúng. Tránh phân tích lan man nhiều biến mà không có định hướng.

8.2. Phân tích những yếu tố không thể kiểm soát

Khi đánh giá mối quan hệ giữa các biến, hãy tự hỏi: “Tôi có thể tác động được không?”

Chẳng hạn, thời tiết hay chương trình của đối thủ là yếu tố ngoài tầm tay, phân tích chúng sẽ ít giá trị thực tiễn. Thay vào đó, nên tập trung vào những yếu tố có thể điều chỉnh như chính sách khuyến mãi, chiến lược giá hay tính năng sản phẩm.

=>> Bài học: Ưu tiên phân tích các biến có thể dẫn đến hành động cụ thể và quyết định chiến lược.

8.3. Dữ liệu không đáng tin cậy

Phân tích hồi quy rất nhạy với dữ liệu. Dữ liệu sai lệch hoặc kém chất lượng có thể khiến kết quả phân tích sai hoàn toàn.

Tùy vào mức độ quan trọng của quyết định, yêu cầu về độ chính xác của dữ liệu cũng khác nhau. Thử nghiệm ý tưởng marketing có thể chấp nhận một số sai sót nhỏ. Nhưng nếu bạn đang ra quyết định hàng triệu đô, dữ liệu cần cực kỳ chính xác.

=>> Bài học: Luôn đánh giá kỹ nguồn dữ liệu, phương pháp thu thập và các giới hạn. Đừng vội tin vào kết quả nếu đầu vào không đáng tin cậy.

8.4. Bỏ qua sai số của mô hình

Một sai lầm phổ biến là quá tin vào kết quả hồi quy mà quên rằng mọi mô hình đều có sai số. Điều này khiến bạn dễ lầm tưởng rằng mối quan hệ là chắc chắn tuyệt đối, trong khi hồi quy chỉ mang tính xác suất.

Ví dụ: Nếu mô hình chỉ giải thích được 10% biến động, nhưng bạn hành động như thể là 90%, hậu quả có thể rất nghiêm trọng.

=>> Bài học: Luôn xem xét các chỉ số như R-squared, khoảng tin cậy… và hiểu rằng hồi quy chỉ cho thấy khả năng ảnh hưởng, không phải sự chắc chắn.

8.5. Lệ thuộc vào dữ liệu, bỏ qua trực giác

Mô hình tốt đến đâu cũng cần kiểm chứng lại với hiểu biết thực tế. Nếu kết quả mâu thuẫn với trực giác hoặc kinh nghiệm thị trường, hãy kiểm tra lại dữ liệu, mô hình và mức sai số.

Một kết quả bất ngờ có thể do lỗi hoặc cũng có thể là mối quan hệ mới – nhưng đừng vội tin nếu chưa đối chiếu thực tế.

 =>> Bài học: Kết hợp dữ liệu với trực giác và kinh nghiệm. Đừng để con số làm lu mờ sự hiểu biết thực tiễn.

9. Kết luận

Hiểu được phân tích hồi quy là gì chính là bước đầu để bạn tiếp cận với thế giới phân tích dữ liệu một cách có hệ thống và khoa học hơn. Dù là trong học thuật hay trong thực tế công việc, phương pháp này giúp chúng ta nhìn thấy rõ hơn mối liên hệ giữa các yếu tố, từ đó đưa ra quyết định chính xác hơn. Nếu bạn đang bắt đầu học thống kê hoặc muốn ứng dụng dữ liệu vào công việc, đừng bỏ qua công cụ phân tích mạnh mẽ này nhé!